有理数集包括什么（集合的概念）

100次浏览发布时间：2024-09-05 09:34:34

1. 集合的概念：我们把研究对象统称元素，把一些元素组成的总体叫做集合(简称集).

2. 集合中元素的特性：

（1）确定性：集合的元素必须是确定的.任何一个对象都能明确判断出它是或者不是某个集合的元素.

（2）互异性: 集合中的任意两个元素都是不相同的,也就是同一个元素在集合中不能重复出现.

（3）无序性: 集合与组成它的元素顺序无关.

3. 集合与元素的关系：若a是集合A的元素，就说a属于A，记作a∈A；若a不是集合A的元素，就说a不属于A，记作a∉A.

4. 集合的表示法：

（1）列举法:把集合的元素一一列举出来，并用花括号“{ }”括起来，基本形式为 { a1，a2，a3，…，an}，适用于有限集或元素间存在规律的无限集.

（2）描述法:用集合所含元素的共同特征来表示，基本形式为{x∈A | P（x）}，既要关注代表元素x，也要把握其属性P（x），适用于无限集.

（3）图示法:韦恩(英国逻辑学家，John．Venn)图(几何方法)：用一条封闭的曲线的内部来表示一个集合的方法.

5. 常用的数集及其记法：

（1）非负整数集(自然数集)：全体非负整数的集合。记作N．N={0,1,2,3，…}

（2）正整数集：非负整数集内排除0的集。记作N*或N+．N*={1,2,3，…}

（3）整数集：全体整数的集合。记作Z．Z={0,±1,±2,±3，…}

（4）有理数集：全体有理数的集合。记作Q．

（5）实数集：全体实数的集合。记作R．

6. 集合的分类：

（1）按集合中所含元素的个数分类

有限集：含有有限个元素的集合.

无限集：含有无限个元素的集合.

空集：不含任何元素的集合. 记作∅，如：{x| x²+1=0，x∈R}.

（2）按集合中元素的性质分类

数集：集合中元素是数值。如

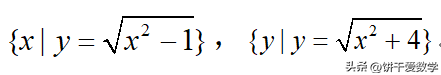
点集：集合中的元素是点。如

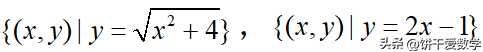
图形集等等.